జర్నల్ ఆఫ్ జెనరలైజ్డ్ లై థియరీ అండ్ అప్లికేషన్స్

In this perspective paper, I tried to explain that what will be the possible prospect of multiple functions in one and another through the chain rule of differentiation? The chain rule is a formula to compute the derivative of the functional composition of two or more functions. The chain rule provides us a technique for finding the derivative of composite functions, with the number of functions that make up the composition determining how many differentiation steps are necessary. The chain rule in that what changes I noted, how it can be modified to reduce the differentiation process of multiple functions in one and another, and implementing that process in the inverse of multiple functions in one and another, further proceedings them through the chain rule of differentiation with all prospects. Here I claim that the differentiation’s chain rule is not changed but the sequences of finding the derivative of multiple functions are changed.

In this paper titled 'The Intersect Point Theorem,' I had performed many mathematical operations on a figure formed by three non-collinear points called a triangle. In this paper
a concept, when two lines intersect at a common point on one of the segments of the triangle, then their cause is defined. I had tried to keep my work in the ordinary language
of Geometry. All these principles keep me on researching various geometrical concepts throughout the year.

In this work, a new class of functions over the quaternions was defined. The initial coefficient bounds for the class defined were obtained. The work was concluded by establishing the Fekete-Szego˙ functional. AMS Mathematics Subject Classification (2010): 30C45, 30G45.

A spray S on the tangent bundle TM with a n dimensional differentiable manifold M defines an almost product structure Γ (Γ² =I, I being the identity vector 1-form) and decomposes the TTM space into a direct sum of horizontal space (corresponding to the eigenvalue +1) and vertical space (for the eigenvalue -1). The Lie algebra of projectable vector fields whose Lie derivative vanishes the spray S is of dimension at most n² +n. The elements of the algebra belonging to the horizontal nullity space of Nijenhuis tensor of Γ form a commutative ideal of . They are not the only ones for any spray S. If S is the canonical spray of a Riemannian manifold, the symplectic scalar 2-form Ω which is the generator of the spray S defines a Riemannian metric g upon the bundle vertical space of TM. The Lie algebra of infinitesimal isometries which is written 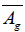contained in is of dimension at most 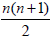. The commutative ideal of is also that of . 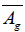The Lie algebra 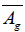of dimension superior or equal to three is semi-simple if and only if the nullity horizontal space of the Γ Nijenhuis tensor is reduced to zero. In this case, Ag is identical to . Mathematics Subject Classification (2010) 53XX • 17B66 • 53C08 • 53B05ns.